- orthogonal
-
orthogonal, ale, aux [ ɔrtɔgɔnal, o ] adj.• 1520; du lat. d'o. gr. orthogonus « à angle droit »♦ Géom. Qui forme un angle droit, qui se fait à angle droit. ⇒ perpendiculaire. Deux droites orthogonales. Vecteurs orthogonaux deux à deux. — Projection orthogonale : projection d'une figure obtenue au moyen de perpendiculaires abaissées à partir des différents points de cette figure sur une droite, un plan, une surface quelconque. ⇒ orthographique, 2o.
● orthogonal, orthogonale, orthogonaux adjectif (latin orthogonus, à angle droit) Se dit de certaines affinités, projections ou symétries telles que les plans ou droites affines servant à les définir sont orthogonales. Se dit de deux courbes, d'une courbe et d'une surface, ou de deux surfaces sécantes, telles que les tangentes, la tangente et le plan tangent ou les deux plans tangents en leur point commun sont orthogonaux. Se dit de deux droites, plans, etc., affines dont les directions sont orthogonales. (Pour deux droites, la différence entre « orthogonales » et « perpendiculaires » est que dans le second cas elles sont forcément sécantes, contrairement au premier.) Se dit de deux vecteurs x et y d'un espace vectoriel E, tels que, f étant une forme bilinéaire symétrique de E, f (x, y) = 0. ● orthogonal, orthogonale, orthogonaux (expressions) adjectif (latin orthogonus, à angle droit) Plan orthogonal, en urbanisme, synonyme de damier. Symétrie orthogonale, symétrie par rapport à une droite, ou à un plan, parallèlement à une direction orthogonale à cette droite, à ce plan. ● orthogonal, orthogonale, orthogonaux (synonymes) adjectif (latin orthogonus, à angle droit) Plan orthogonalSynonymes :- damierorthogonal, ale, auxadj. GEOM Qui forme un angle droit; qui se fait à angle droit. Plans orthogonaux, qui se coupent à angle droit. Projection orthogonale, obtenue au moyen des perpendiculaires abaissées des différents points d'une figure au plan de projection.⇒ORTHOGONAL, -ALE, -AUX, adj.GÉOM. Qui forme un angle droit, qui tombe à angle droit. Synon. perpendiculaire. Si le plan du diapason est orthogonal au fil (excitation transversale) il y a (...) accord à l'unisson (Hist. gén. sc., t.3, vol. 1, 1961, p.199).♦Droites orthogonales, plans orthogonaux. Droites, plans qui se coupent à angle droit.♦Courbes, ellipses, hyperboles orthogonales. Courbes, ellipses, hyperboles dont les tangentes respectives forment un angle droit à leur point d'intersection. Cette fonction fournit justement dans le plan de section droite des ellipses et des hyperboles orthogonales (FRÜHLING, Cours d'électr., t.1, 1966, p.69).♦Projection orthogonale. Projection d'une figure suivant des perpendiculaires abaissées, à partir de ses différents points, sur un axe ou un plan. Synon. orthographie, projection orthographique. La hauteur totale du crâne et sa largeur maxima, la largeur de la face, la largeur orbitaire, la largeur de la mâchoire inférieure, toutes ces dimensions sont mesurées en projection orthogonale (Hist. sc., 1957, p.1365).REM. Orthogonalement, adv. Perpendiculairement, à angle droit. Les cercles de l'espace qui passent par un point fixe et coupent orthogonalement en deux points un cercle donné (Gds cour. pensée math., 1948, p.51).Prononc. et Orth.:[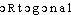
], plur. masc. [-o]. Att. ds Ac. dep. 1762. Étymol. et Hist. 1520 triangle orthogonal (EST. DE LA ROCHE, Arithm., f° 226 v°); 1554 ligne orthogonale «ligne perpendiculaire (à une autre)» (PELETIER DU MANS, Algèbre, 20 d'apr. FEW t.7, p.422); 1562 id. (BULLANT, Horolog., p.8 ds GDF. Compl.); 1868 «qui se fait à angle droit (d'une projection)» (LITTRÉ). Dér. du gr. 
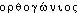«à angle droit, rectangulaire; rectangle (d'un triangle)», cf. lat. orthogonius «id.».DÉR. Orthogonalité, subst. fém. État de courbes, de droites, de projections, etc., qui sont orthogonales. La notion d'«orthogonalité» correspondante s'introduit au moyen de l'angle droit (BOURBAKI, Hist. math., 1960, p.130). — [
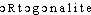]. — 1re attest. 1948 (Gds cour. pensée math., p.132); de orthogonal, suff. -(i)té.orthogonal, ale, aux [ɔʀtɔgɔnal, o] adj.ÉTYM. 1520; dér. sav. du lat. orthogonus « à angle droit », grec orthogônios; → -gone, -gonal.❖♦ Géom. Qui tombe, qui se fait à angle droit; qui forme un angle droit. ⇒ Perpendiculaire. || Droites orthogonales : droites perpendiculaires entre elles. || Plans orthogonaux. || Courbes orthogonales : courbes qui ont un point commun et dont les tangentes respectives menées par ce point sont perpendiculaires entre elles — Projection orthogonale (ou orthographique) : projection d'une figure obtenue au moyen de perpendiculaires abaissées à partir des différents points de cette figure sur une droite, un plan, une surface quelconque. ⇒ Orthographie.❖DÉR. Orthogonalement.
Encyclopédie Universelle. 2012.
